论文主体思路

论文主要贡献

  1. 通过在自由空间中一次性检测光场穿过二维斐波那契光栅前物体的远场强度分布，可以检索到空间分辨率超过λ/7的物体图像。
  2. 空间分辨率表征成像系统的最小可分辨能力，一般认为二维(2D)系统为0.61λ/NA，一维(1D)系统为0.5λ/NA。
  3. 亚波长结构用于将前方物体的倏逝波转换为远场探测所需的传播波。此外，这种亚波长结构还可以产生倏逝波，照亮分辨率以下尺度的物体，从而进一步从物体的散射光或衍射光中获取超分辨率图像。
  4. 周期亚波长光栅的一个关键缺陷，它只能产生固定的相移，使频域不连续。为了克服这一缺点，可以使用一种准周期亚波长光栅在频域内产生准连续位移。由于空间频域是连续的，在一定空间频率范围内丢失的亚波长信息可以被携带到远场区域。因此，可以利用远场检测信息重建超分辨率图像。
  5. 本文提出了一种用于自由空间远场超分辨率成像的二维斐波那契光栅辅助显微镜。采用严格耦合波分析(RCWA)方法对二维斐波那契光栅进行设计和优化，将二维物体的倏逝波转化为传播波。通过一次测量远场光强分布，我们可以通过傅里叶光学方法和时域有限差分(FDTD)数值模拟方法重建空间分辨率超过λ/7的样品物体图像。与用于扩展一维空间频率轴连续的一维斐波那契光栅辅助显微镜相比，我们的二维斐波那契光栅可以使二维空间频率圆平面上的频域连续。因此，所有低于该分辨率的具有不同亚波长细节的二维图像都可以被分辨出来。

基础理论

二维斐波那契光栅理论设计

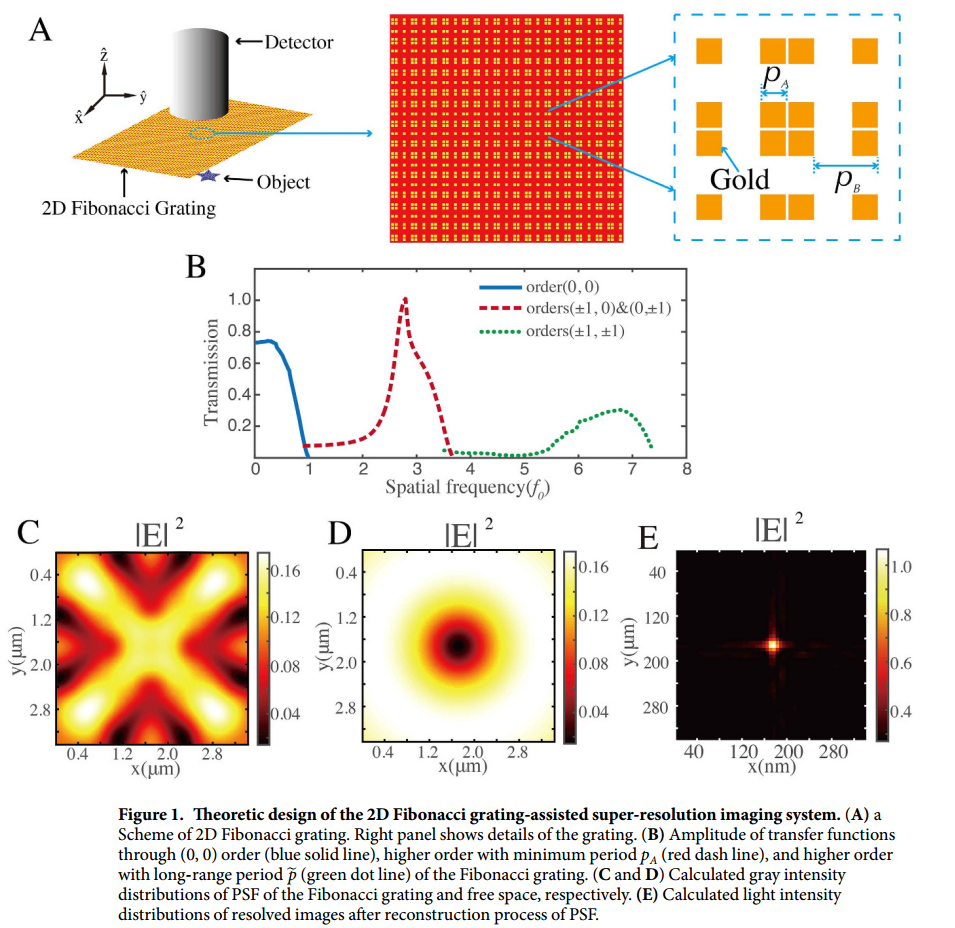
  1. 每个光栅单元都是亚波长块，因此光栅将显示出与偏振无关的正常入射响应20。在每一行和每一列中，沿着x´和y´方向，两个基本单位以斐波那契级数的形式排列为“…abaababababababab…”。

相干光照条件下仿真结果

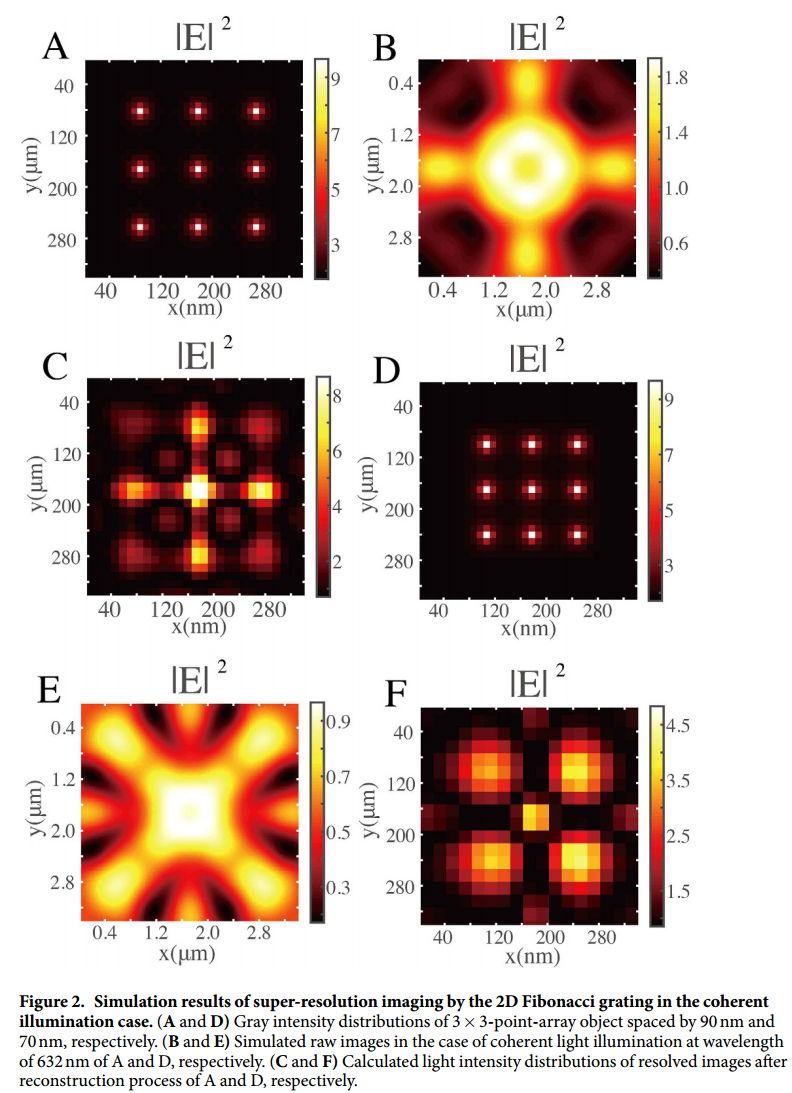
  1. 相干光照下二维斐波那契光栅超分辨率成像的仿真结果。(A、D)分别间隔90nm和70nm的3×3-point-array物体灰度分布。(B)和(E)分别为A和D波长为632nm的相干光照射下的模拟原始图像。(C、F)分别计算A、D重建过程后的分辨图像光强分布。

非相干光照条件下仿真结果

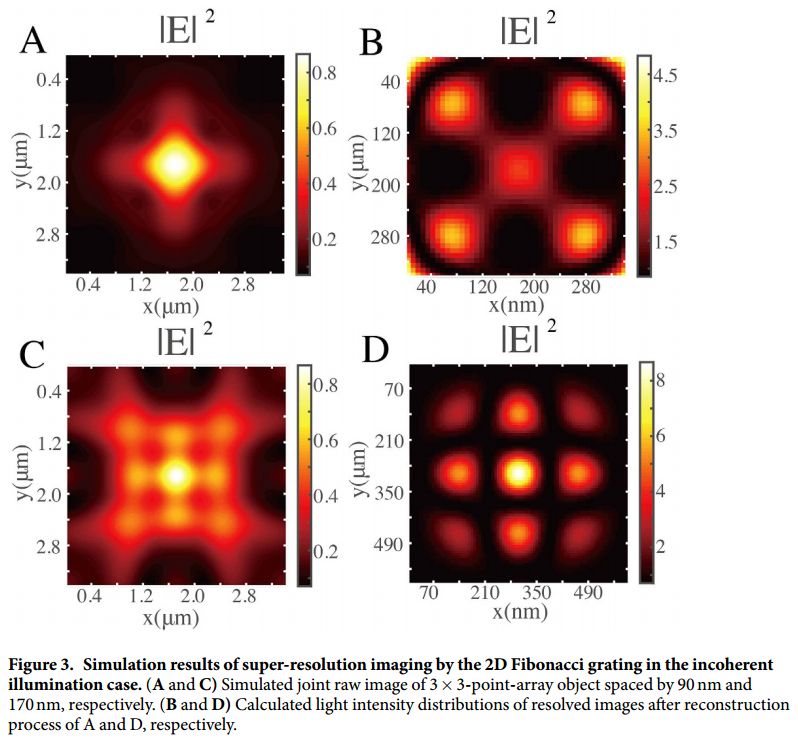
  1. 非相干光照条件下二维斐波那契光栅超分辨率成像的仿真结果。(A、C)分别间隔90nm、170nm的3×3-point-array物体模拟关节原始图像。(B、D)分别计算A、D重建过程后的分辨图像光强分布。

反卷积过程

附录与补遗

论文中可以引用的部分

无。

关于文献

题目及期刊

题目：Two-dimensional Fibonacci grating for far-field super-resolution imaging

用于远场超分辨率成像的二维斐波那契光栅

期刊：Sci Rep

作者信息

作者：K. Wu , G. P. Wang

发表时间

日期：2016年

阅读时间

日期：2024年9月24日

开源代码及其它

GitHub：无