论文主体思路

论文主要贡献

图案照明傅立叶压印术（piFP）是结构照明成像和傅立叶压印算法的优雅结合，具有超越所采用光学器件衍射极限成像的能力。无伪影的piFP超分辨率重建要求光照模式的高度稳定性。
在存在环境扰动、强度波动和指向源不稳定的情况下，会发生不可预测的模式变化，导致图像重建质量下降。为了解决这一问题，我们提出了一种基于低秩近似的高效鲁棒piFP算法（LRA-piFP），该算法放宽了对照明模式稳定性的要求。
计算成像（CI）技术使成像能够通过散射介质，和绕过光学的衍射限制。CI的原理是共同设计物理编码模型和计算解码算法，允许从间接测量中重建图像。在CI中，解逆图像重建往往需要对物理模型有准确的了解。然而，在许多实际情况下，理论模型与现实物理系统之间存在差异，导致模型不匹配，从而带来令人不快的伪影，降低重建质量。因此，考虑模型不匹配对提高CI的可靠性和适用性至关重要。
为了实现高质量的图像重建，结构照明显微镜（SIM）需要准确估计初始相位和调制深度等照明参数。即使很小的参数错误也会导致重大的重建伪影由于这个原因，已经提出了许多算法来估计照明参数。另一个例子是傅里叶平面摄影（FP），这是一种新颖的CI技术，可以绕过所用光学器件的衍射极限。
由于频率混合效应，每个原始图像包含超出成像镜头截止频率的信息，并且可以恢复超分辨率样本图像以及照明模式。
piFP的重建过程与FP有共同的根源，FP在空间和傅里叶空间之间迭代切换，从一组低分辨率测量中恢复高分辨率图像。因此，FP的许多算法扩展也适用于piFP。
在piFP中，光照模式在样品上被顺序扫描，而其分布假定是平稳的。然而，导致模式变化的原因有很多，包括环境扰动、光源方向不稳定和功率，导致模型不匹配，从而阻碍图像的准确重建。这种光照模式的不匹配在piFP实现中很常见，但据我们所知，这仍然是一个未解决的问题。为了解决这个问题，我们提出了一种基于低秩近似的高效鲁棒piFP算法，称为LRA-piFP，在不做任何事先假设的情况下对模式变化进行建模。LRA-piFP方法通过在每个扫描位置重建不同的模式来放松平稳模式假设。在迭代重建过程中，所有扫描位置的模式被投影到由截断奇异值分解（SVD）确定的低维空间中。在低维空间中，每个扫描位置的模式被估计为几个特征模的线性组合，而不必要的和有噪声的模式被拒绝。低秩近似对CI技术来说并不新鲜；它背后的思想是“降维”，它已被用于传统的平面摄影（CP）来模拟时间探针的变化，在FP中用于考虑瞳孔的空间变化，在相位检索中用于抑制噪声，和在SIM中用于估计照明参数。
第二节描述了piFP的前向模型和我们用于恢复具有不同模式的高质量超分辨率图像的LRA-piFP算法；第三节给出了LRA-piFP方法的仿真结果；第四节通过在远程成像中使用USAF靶标和在光学显微镜中使用Siemens星靶来量化图像质量的改善，并将LRA-piFP与原始piFP以及blind-SIM的性能进行比较。

频率混合效应（Frequency Mixing Effect）

频率混合效应是由于成像系统的截止频率（或称空间频率的上限）所引起的现象。在成像系统中，镜头的成像能力是有限的，无法捕捉到超过某个频率的高频信息。超出镜头截止频率的频率信息可能会混合或丢失，导致图像模糊或细节丢失。
在超分辨率显微镜技术中，尤其是结构光显微镜（SIM），这一效应是非常常见的。因为照明模式的设计（如使用不同的照明频率）有助于恢复原始图像中的高频信息。通过对多幅不同频率的图像进行组合处理，可以恢复被丢失的高频细节，从而提高图像的空间分辨率。

piFP的前向模型

图样照明傅立叶平面照相术原理。(a)实验设置。(b)高分辨率物体。(c)光照模式不均匀。(d)物体和图案的乘法。(e) (d)的傅里叶谱。(f)光学传递函数。(g)低分辨率原始图像。FT和IFT分别表示傅里叶变换和傅里叶反变换。
piFP方法使用非均匀强度模式对样品进行扫描，并通过成像透镜捕获相应的低分辨率图像。在这里，强度模式在数字微镜设备（DMD）上播放，并通过投影透镜投射到物体上。与SIM类似，照明图案和物体之间的混频效应导致高频采样信息转移到低频通带。因此，每个捕获的图像Ik(x)包含的信息超出了成像透镜的衍射极限。
图1(b) -1 (g)总结了正向过程，式中，x为空间坐标，xk为图像的偏移量，O(x)为物体，P（x−xk）为第k个光照模式，psf为集体光学确定的强度点扩散函数，“⋅”为逐元乘法。⋆是卷积算子，Eq.(1)中的卷积运算通常通过快速傅里叶变换在傅里叶域中计算。

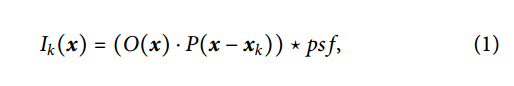
(1)式假设模式运动时物体是静止的，这与CP中探针-物体的相互作用类似。为了建立静止模式模型，我们可以将Eq.(1)等效表示为物体相对于模式的运动。令x ‘ = x−xk，则方程修改为式2，其中Ik（x′+ xk）为移位图像，可以根据偏移量xk对捕获图像进行简单的平移。

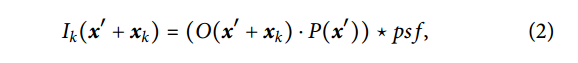
重建图像

关于文献

题目及期刊

题目：Toward robust super-resolution imaging: A low-rank approximation approach for pattern-illuminated Fourier ptychography

迈向稳健的超分辨成像：模式照明傅立叶平面摄影的低阶近似方法

期刊：APL Photonics

引用

Zhang, Junhao, et al. “Toward Robust Super-Resolution Imaging: A Low-Rank Approximation Approach for Pattern-Illuminated Fourier Ptychography.” APL Photonics 9.6 (2024). Print.

作者信息

作者：Junhao Zhang，Weilong Wei，Kaiyuan Yang，Qiang Zhou，Haotong Ma，Ge Ren，Zongliang Xie

发表时间

日期：2024年

阅读时间

日期：2024年11月18日

开源代码及其它

GitHub：无