论文主体思路

论文主要贡献

  • 提出了一种以光学成像物理过程为导向的物像平面退化网络（OIDN）。具体来说，提出的OIDN将目标到图像平面的退化过程嵌入到重建网络中，以提供明确的指导。OIDN利用一组受物理先验约束的可学习点扩展函数（PSF）参数，成功地将传统的图像到图像的数据模式映射转化为高度符合SIM成像光学过程的物体到图像的平面退化映射。
  • 基于深度学习的SIM重建算法存在两个主要问题：1)重建结果可信度有限：基于DL的重建算法被表示为“黑盒”，使得神经网络如何从有限的输入中产生预期结果变得不清楚，甚至导致错误的重建结构的出现；2)重构模型的泛化性低：这是由于端到端深度学习方法的泛化性与训练样本的大小和种类密切相关。
  • 提出了一种称为目标到图像平面退化网络（OIDN）的方法。由于SIM系统[31]中照明模式和点扩展函数（PSF）的固有性质，PSF信息隐式编码在微观标本[32]的图像中，这些信息可以用于设计符合SIM物理模型的网络。OIDN基于SIM成像系统的物理退化模型，利用原始输入图像、噪声分量和可学习的PSF构建了一个接近真实的退化过程。此外，为了严格按照SIM成像过程的原理对网络进行优化，利用物理先验来约束PSF的生成，从而在有限的训练数据下获得具有高泛化性的模型。

空间物理退化过程

  • 正是PSF的卷积运算导致了高频信息的丢失。

频率物理退化过程

SIM重构过程的物理模型

物像平面退化网络

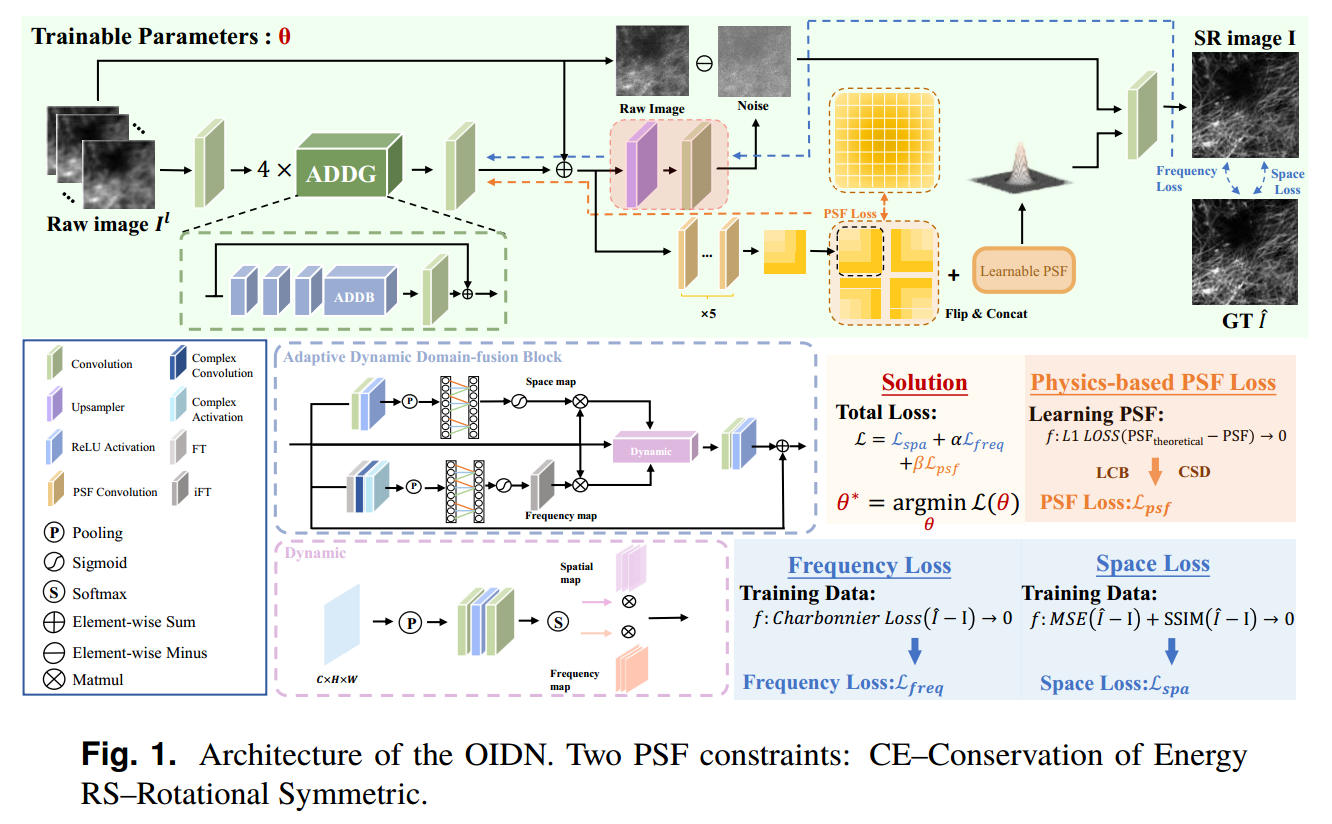
  1. 该过程从3×3卷积层开始，该层将输入的原始图像D(r)转换为多维特征空间。随后，这些特征被输入到一个由四个自适应动态域融合组（ADDG）组成的模块中，每个组都配备了剩余连接。该设计策略性地规避了在过深网络中可能出现的梯度消失问题，从而使网络能够更有效地集中于高频特征的学习。每个ADDG模块由四个自适应动态域融合块（ADDB）、一个3 × 3卷积层和一个短跳接组成。ADDB采用双分支结构，构建动态权值机制减少频域信息损失，采用全局平均池化提取信号整体趋势，全局最大池化重点捕获重要局部特征，实现频域特征的自适应调整。

损失函数

模型的性能不仅取决于其结构，而且还受损失函数的选择的显著影响。认识到这一点，我们制定了一个全面的总损失函数，有效地利用输入图像中固有的高频和低频信息。具体来说，它包括三个不同的组成部分：空间域损耗、频率域损耗和PSF损耗。

损失函数示意图看图1右下角！！！

空间损失函数

由均方误差（MSE）损失[22]和结构相似指数度量（SSIM）损失[37]组合而成的空间域损失函数保证了像素精度，平衡了预测动态范围，并增强了输出图像的结构相似性。若将S(r)定义为SR模型的输出，将S(r)‘ 定义为相应的GT，将（w, h）定义为输出图像的像素大小，则目标函数可表示为：

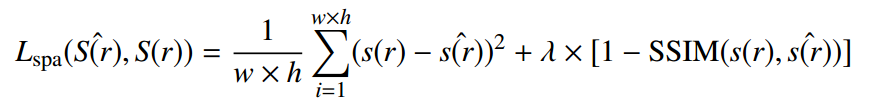
其中λ是用于平衡SSIM和MSE相对贡献的标量权重，在本文中大多数情况下设置为0.1。

代码

``

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def loss_mse_ssim(y_true, y_pred):
    ssim_para = 1e-1
    mse_para = 1

    # nomolization
    x = y_true
    y = y_pred
    # x = norm(x)
    # y = norm(y)
    MSE_loss = nn.MSELoss()
    MSE_loss = MSE_loss.to(device)
    # SSIMloss = SSIM()
    # SSIMloss = SSIMloss.to(device)

    mse_loss = mse_para * MSE_loss(x, y)
    ssim_loss = ssim_para * (1 - pytorch_msssim.ssim(x, y))
    mse_ssim_loss = mse_loss + ssim_loss

    return mse_ssim_loss

频率损失函数

为了增强网络学习和获取频域信息的能力，在频域对预测输出图像和GT图像施加约束。在本研究中，我们采用Charbonnier Loss作为频率损失函数的主成分。这种选择是战略性的，因为Charbonnier Loss以其在管理异常值方面的有效性而闻名，异常值是图像处理中的一个关键方面[38]。此外，它还显著提高了模型在图像生成任务中的收敛速度和整体性能。利用Charbonnier Loss符合我们在精度和计算效率之间取得平衡的目标，从而优化模型产生高质量图像重建的能力。频域损失函数可以表示为：

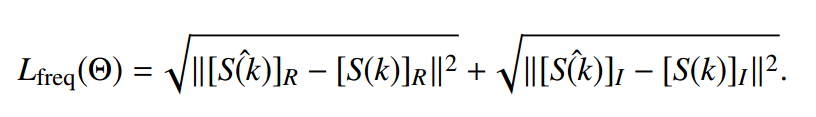
Charbonnier 损失函数

``

1
2
3
4
5
6
def fft2d(input):
    # fft.fftn 是 PyTorch 的多维快速傅里叶变换函数。
    # 参数 dim=(2, 3) 表示对输入张量的第 2 和第 3 维（即高度和宽度）进行二维傅里叶变换。
    # 参数 norm='ortho' 表示使用正交归一化方式，确保傅里叶变换是能量守恒的。
    fft_out = fft.fftn(input, dim=(2, 3), norm='ortho')
    return fft_out
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def CharbonnierLoss(y_true, y_pred):
    # 定义 Charbonnier 损失的平滑参数
    # epsilon 是 Charbonnier 损失的一个平滑参数，用于避免梯度不稳定问题
    epsilon = 1e-3
    epsilon2 = epsilon*epsilon

    # 对输入进行二维傅里叶变换
    # 对输入的真实值和预测值分别应用二维傅里叶变换，将其从时域信号转换为频域信号。
    # fft2d 函数假定是一个支持 PyTorch 张量的自定义或已导入的函数
    y_true_fft = fft2d(y_true)
    y_pred_fft = fft2d(y_pred)

    # 提取频域的实部和虚部
    # 从傅里叶变换结果中提取真实值和预测值的实部和虚部，用于后续计算。
    yt_real = y_true_fft.real
    yt_imag = y_true_fft.imag
    yp_real = y_pred_fft.real
    yp_imag = y_pred_fft.imag

    # 计算频域损失
    # 分别计算实部和虚部的 Charbonnier 损失，使用 torch.sqrt 和 epsilon2 保持数值稳定。
    # 最终将实部和虚部的损失相加，得到频域损失。
    # 对所有频域值求平均，返回最终的标量损失值。
    real = torch.sqrt(torch.pow((yt_real - yp_real), 2) + epsilon2)
    imag = torch.sqrt(torch.pow((yt_imag - yp_imag), 2) + epsilon2)
    value = real + imag
    return torch.mean(value)

PSF损失函数

PSF模块定义了可学习PSF的最终输出，如图1右上角所示。PSF损失函数被设计用来表征最终输出H ‘ (r)与两个物理约束之间的间隙，促使PSF从正确的分布中学习，式中r≡(x, y)为空间位置向量，n为可学习PSF的大小

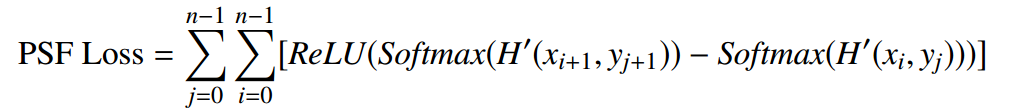
在这种情况下，使用CE损耗和RS损耗分别量化理想PSF与能量一致性和旋转对称分布的偏差。通过不同维度的区分，可以通过评估不同空间背景下的特征来实现对PSF质量的更全面评估。这种方法对于确保PSF在图像重建过程中的准确性和有效性至关重要。

总损失函数

考虑空域、频域和PSF的约束，总损失函数可表示为：

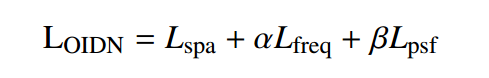
在损失函数中，α和β是平衡参数。在本研究中，它们分别固定为0.01和1 × 10−3。选择这些值是为了平衡损失函数中不同分量的贡献，确保图像重建过程的各个方面之间的最佳权衡。

代码

``

1
2
loss = args.weight*L1_loss(output, gt_images)+(1-args.weight)*torch.abs(1-ssim_loss(output, gt_images))+ (1e-3) * loss_psf + 0.01 * CharbonnierLoss(gt_images, output)
# 此处空间损失函数由论文中的MSE+SSIM换成了L1+SSIM

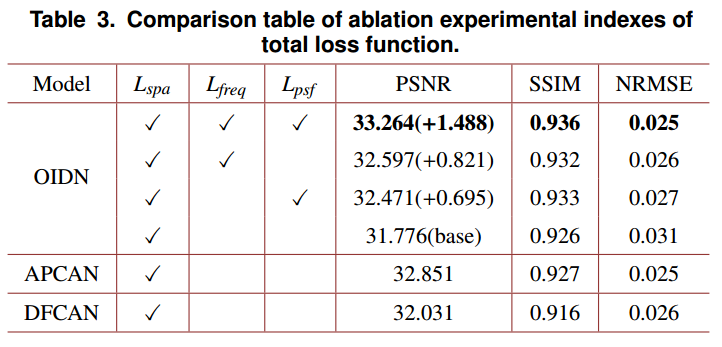
损失函数的消融实验

三种模型的SIM重构能力评价结果

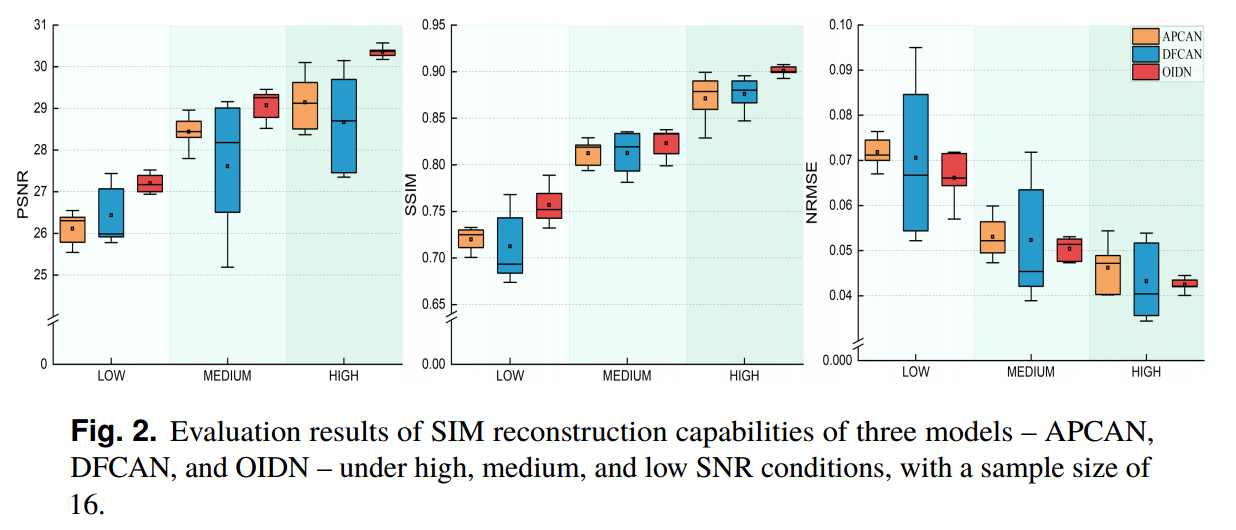
  1. 研究中使用的测试图像根据其荧光激发水平分为高、中、低三类。这种分类是至关重要的，因为它确保了成像结果的保真度与SIM通常应用的真实场景一致。该方法可以更准确地评估每种方法在接近实际使用情况下的性能，为其在SIM重建中的实际适用性和有效性提供有价值的见解。
  2. 为了进一步评价三种方法在重建分辨率方面的性能，我们使用去相关分析（DA）来评估超分辨率图像的分辨率。

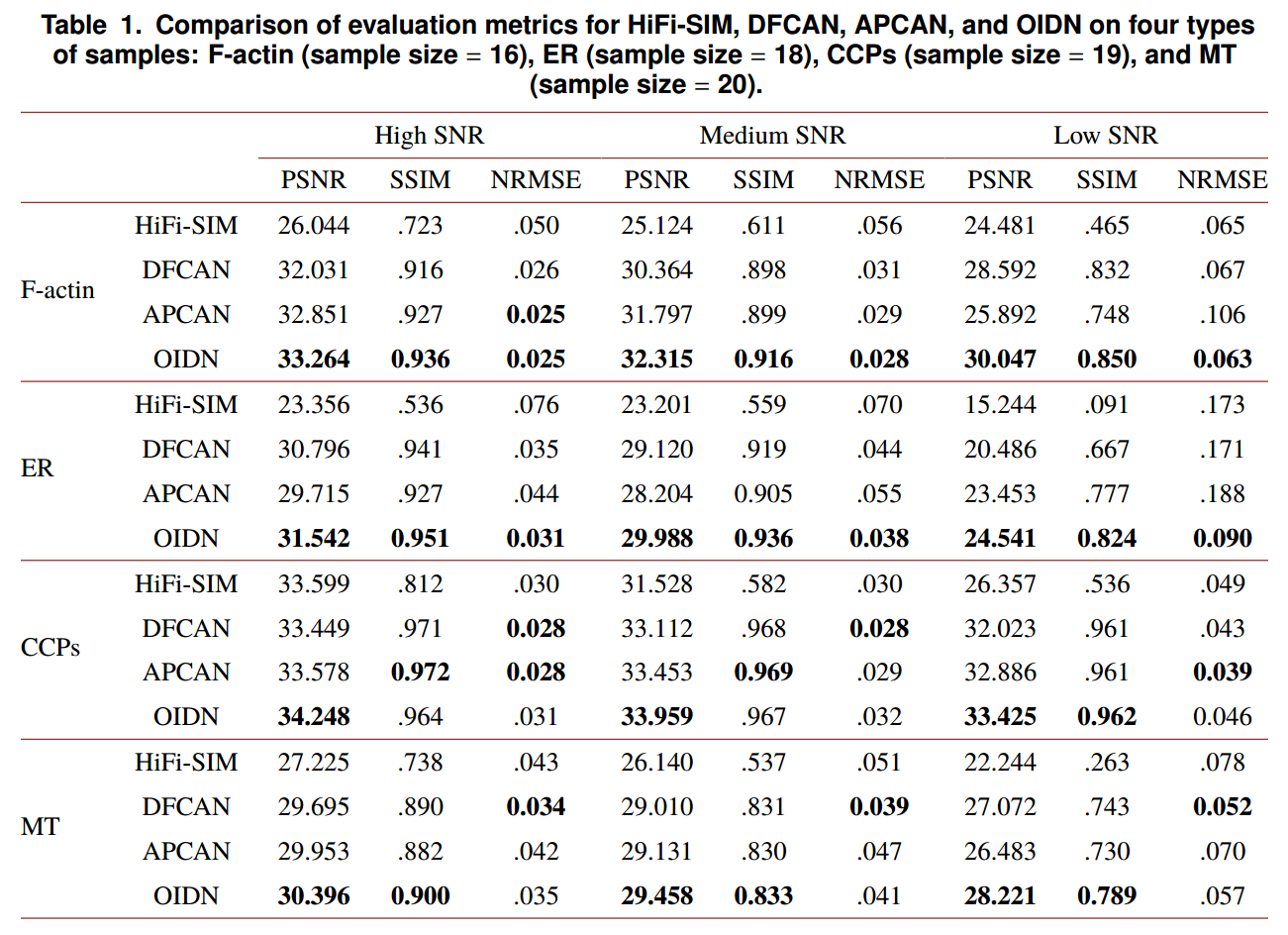
  1. 比较HiFi-SIM、DFCAN、APCAN和OIDN在四种类型样本上的评价指标：F-actin（样本量= 16）、ER（样本量= 18）、CCPs（样本量= 19）和MT（样本量= 20）。

基于去相关分析的SR图像分辨率评价

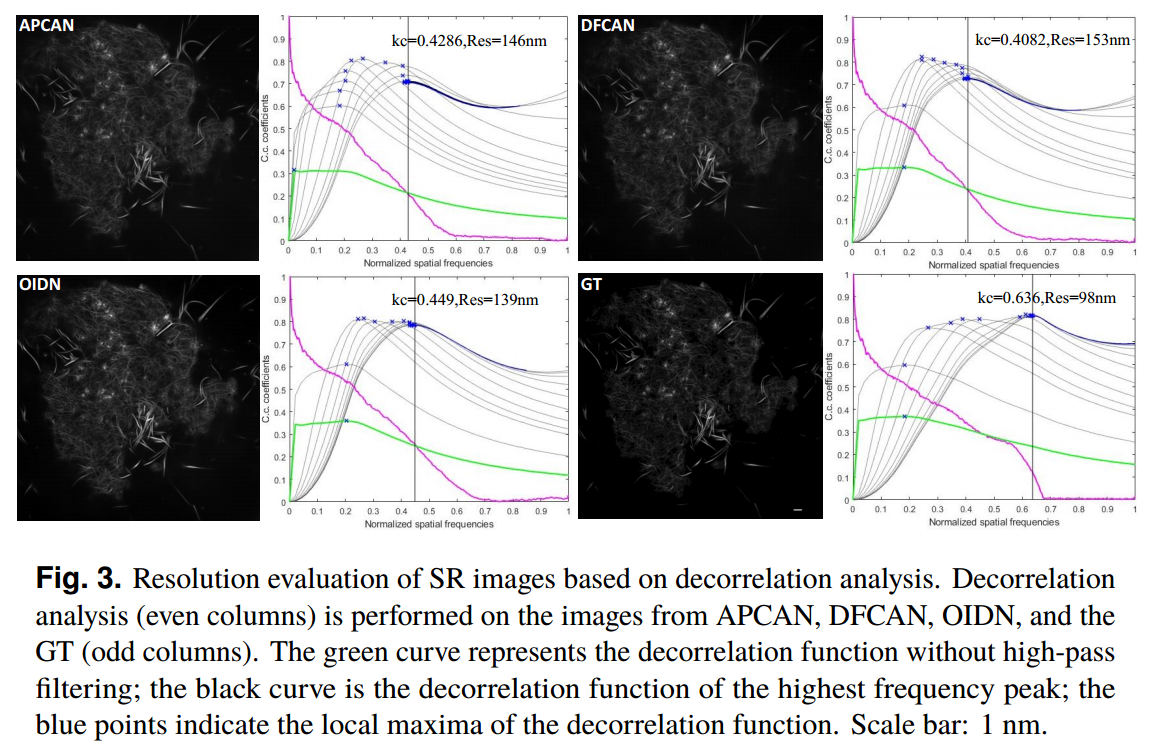
  1. 对来自APCAN、DFCAN、OIDN和GT的图像（奇列）进行去相关分析（偶列）。绿色曲线表示未经高通滤波的去相关函数；黑色曲线为最高频率峰值的去相关函数；蓝色的点表示去相关函数的局部最大值。比例尺：1nm

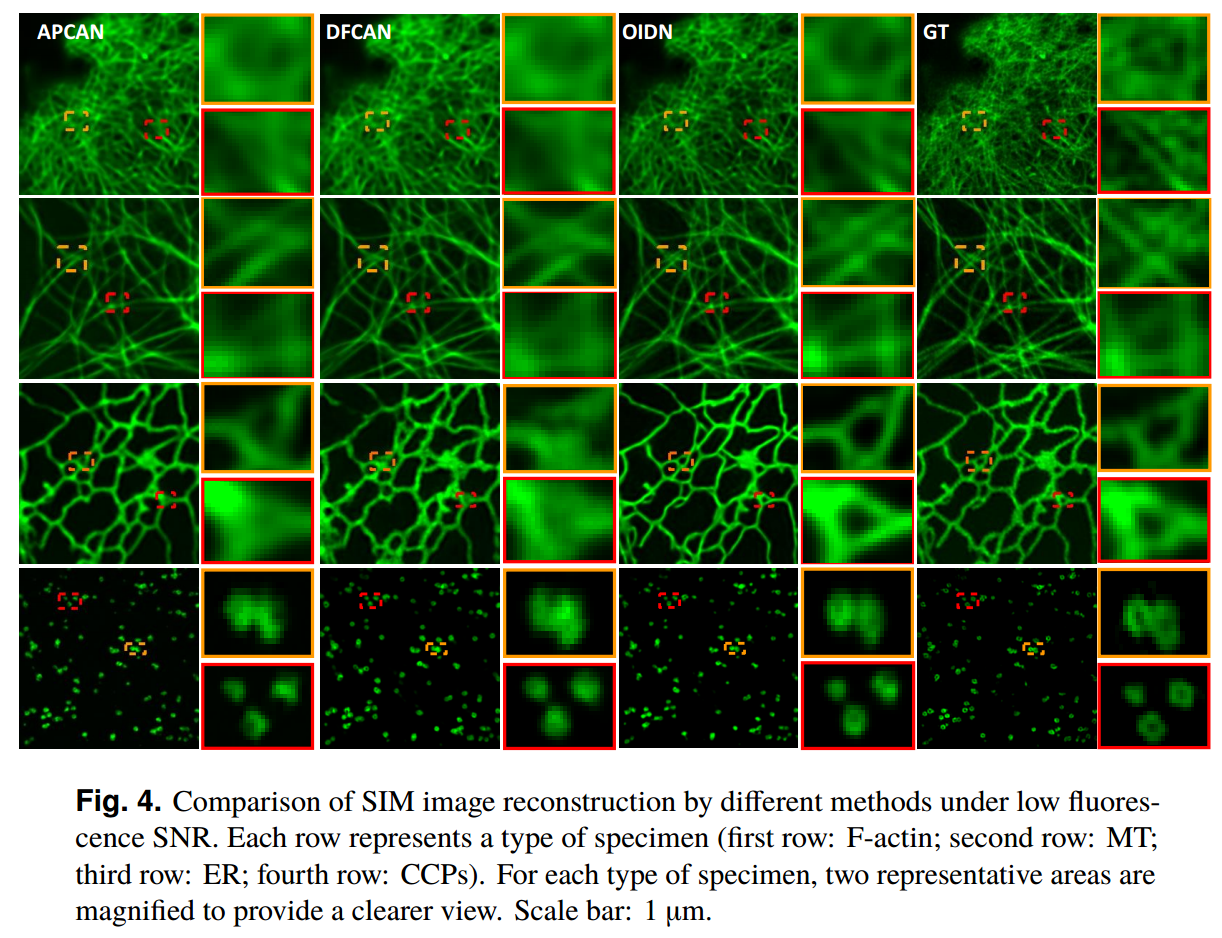
  1. 低荧光信噪比下不同方法重建SIM图像的比较。每行代表一种类型的标本(第一行：F-actin；第二行：MT；第三行：ER；第四行：ccp)。对于每种类型的标本，两个代表性区域被放大以提供更清晰的视图。比例尺：1µm

可信度实验比较

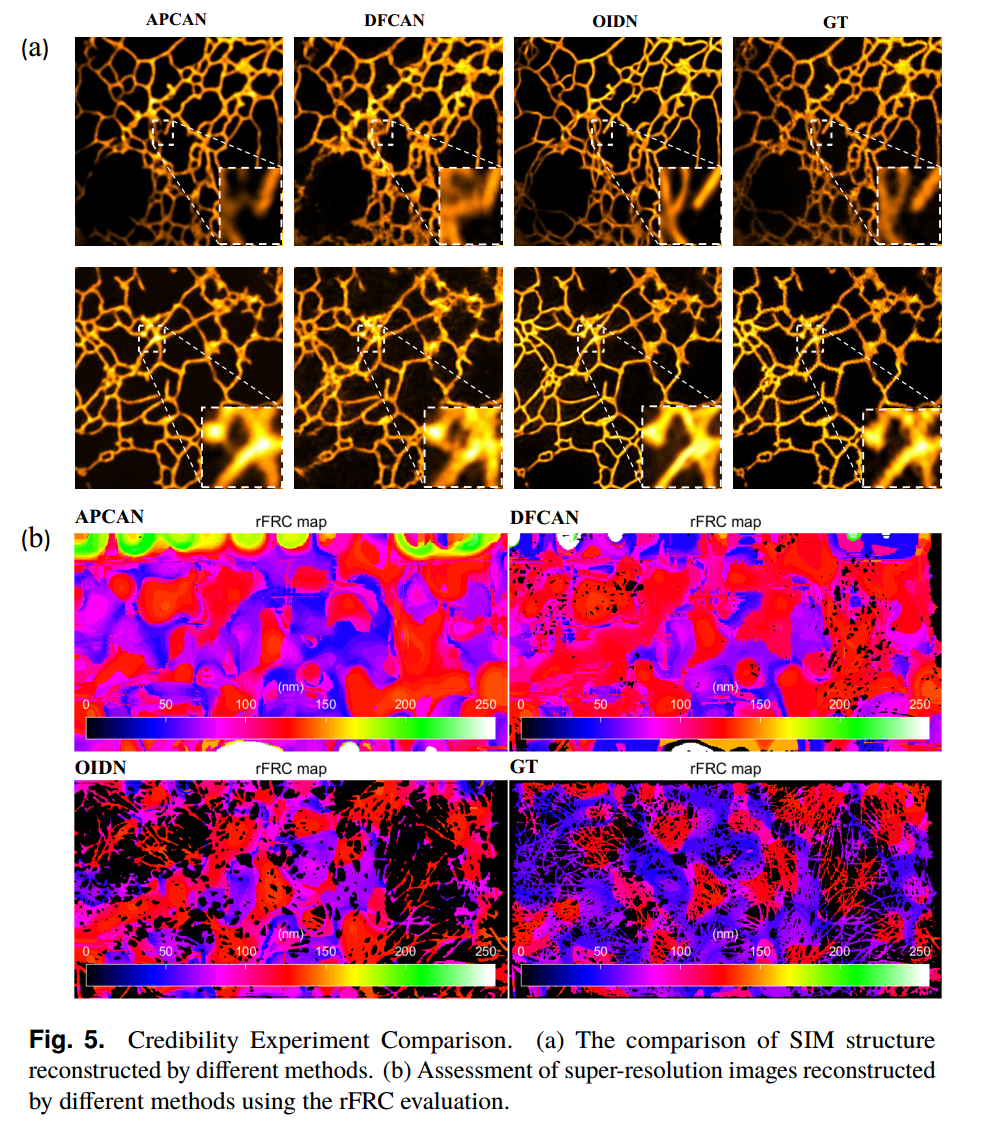
  1. (a)不同方法重构的SIM结构对比。(b)利用rFRC评价评价不同方法重建的超分辨率图像。
  2. 滚动傅立叶环相关（rFRC）[40]方法用于测量傅立叶域中两个信号之间的距离，对强度变化和微运动不敏感。它通过定义最可靠的频率分量来量化重建误差。rFRC通常用于评估重建不确定性至超分辨率尺度，通过局部图像质量的显示更详细地说明图像的重建质量，可以精确识别不同模型输出图像中可靠性较低的区域。
  3. 经过详细计算，APCAN的平均分辨率为100.95 nm，而DFCAN的平均分辨率为102.86 nm。相比之下，OIDN的平均分辨率为99.93 nm，表现出显著的性能提升。
  4. 相比之下，GT的平均分辨率为82.55 nm，可视化如图5(b)所示。OIDN的最大全像分辨率为154.72 nm，较APCAN （568.19 nm）和DFCAN （505.05 nm）有显著提高，更接近GT （139.23 nm）。这表明OIDN重建的图像不确定度更低，重建质量更可靠。

概括性实验比较

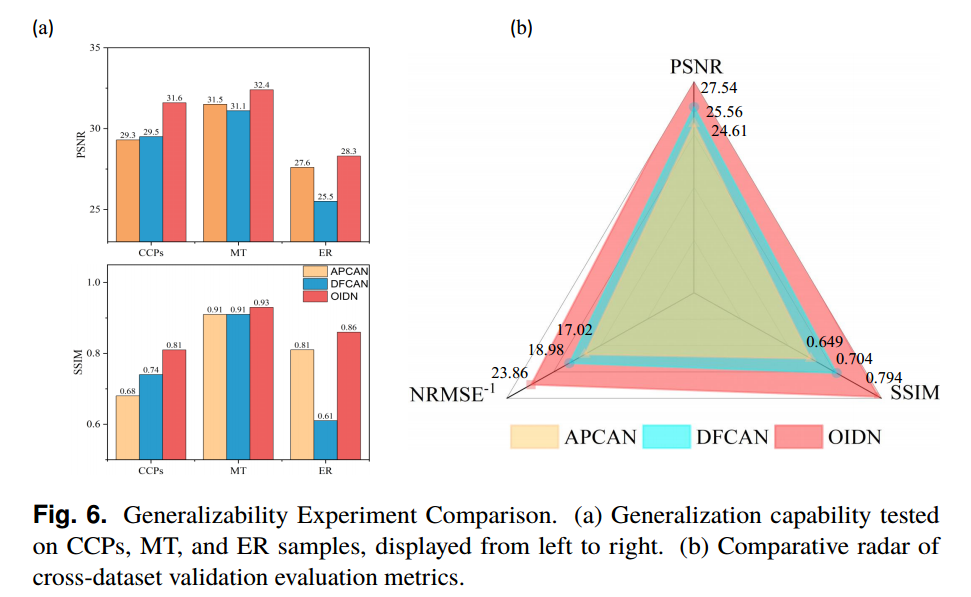
  1. (a) CCPs、MT和ER样本的泛化能力测试，从左至右显示。(b)跨数据集验证评估指标的比较雷达。

理论PSF与可学PSF的比较结果

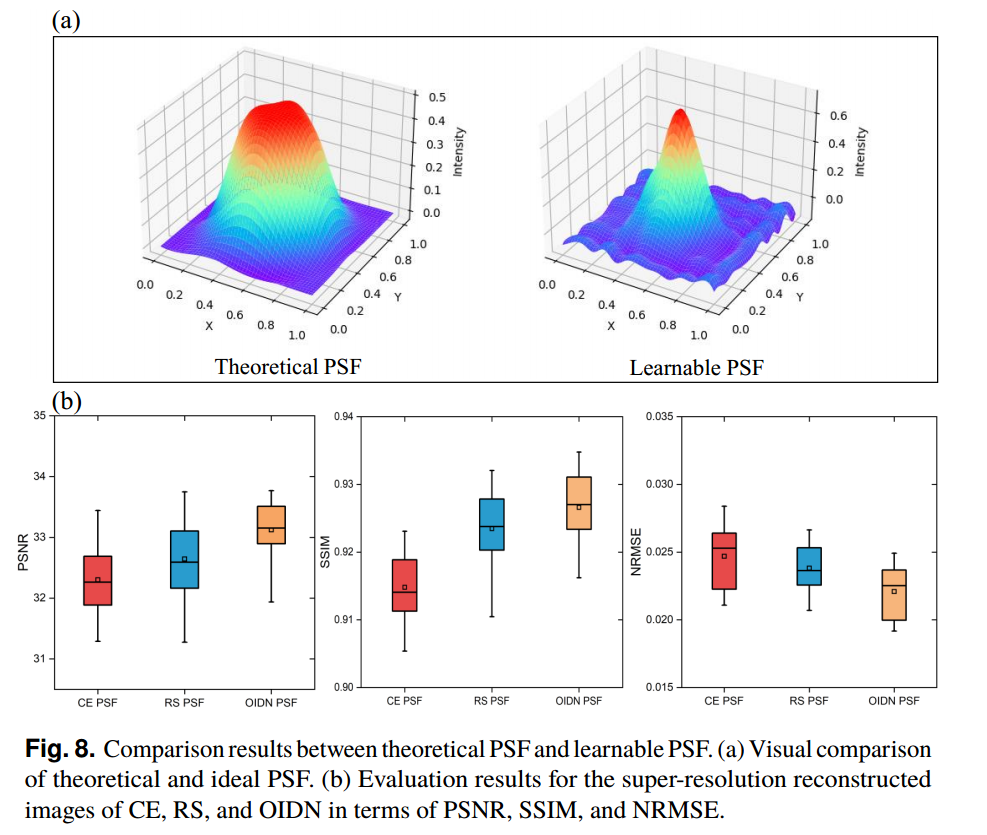
  1. (a)理论和理想PSF的目视比较。(b) CE、RS和OIDN超分辨率重建图像的PSNR、SSIM和NRMSE评价结果。

附录与补遗

滚动傅立叶环相关（rFRC）[40]方法

参考论文

论文中可以引用的部分

关于文献

题目及期刊

题目：Physical prior-guided deep learning for SIM reconstruction: modeling object-to-image degradation

物理先验引导深度学习用于SIM重建：建模对象到图像的退化

期刊：Optics Express

引用

  • Jin, Zitong, et al. “Physical Prior-Guided Deep Learning for Sim Reconstruction: Modeling Object-to-Image Degradation.” Optics Express 32.21 (2024). Print.

作者信息

作者：ZITONG JIN，JUNKANG DAI，BOWEN LIU，ZHIXIANG WEI，ZHENAN FU，HUAIAN CHEN，AND YI JIN

发表时间

日期：2024年

阅读时间

日期：2024年11月19日

开源代码及其它

GitHub：https://github.com/USTCdjk/OIDN/tree/master (作者)