基于倏逝波照明的空间移频超分辨成像技术研究
论文主体思路
论文主要贡献
- 空间移频超分辨成像技术利用样品表面的微纳结构对照明倏逝波的散射, 使其转换为传播波, 并将倏逝波携带的高频空间信息转换成低频信息, 可被远场的显微物镜所接收, 实现超分辨成像。其极限分辨率由照明的倏逝波波长决定, 但分辨率仅在倏逝波波矢方向上有提升。
- 现有的棱镜全反射倏逝波生成方案中, 倏逝波的最短波长受棱镜折射率的限制, 因此其最高分辨率也受限制; 且生成的倏逝波波矢为单一方向, 因此分辨率存在方向差异性。
- 空间移频超分辨成像 (spatial frequency shiftsuper-resolution imaging, SFSSRI)可利用样品表面微纳结构对入射倏逝波的散射, 使之转换成传播波, 进而获取样品表面的超精细空间信息, 其极限分辨率由倏逝波的波长决定。
- 提出一种基于微纳结构的新型倏逝波生成方案, 可突破材料折射率的限制, 实现更短的倏逝波波长. 另外, 所生成的倏逝波具有全方向波矢, 因此在各个方向上具有相同的成像分辨率, 解决了成像分辨率方向差异性问题。
SFSSRI技术及其分辨率极限
- 根据空间频率和分辨率的关系,只要能够获取目标的高频空间信息,即可实现对目标的超分辨成像。 然而,普通的光学成像系统都是低通滤波器,超过物镜自身截止频率K_max的高频信号都无法进入物镜。截止频率对应的空间距离,即为成像物镜的极限分辨率。
结构光照明技术
结构光照明技术, 物镜接收到的空间频率 K_rec 为样品空间表面结构的空间频率 K_obj 与照明光场空间频率K_ill 的差频信号, 即
K_rec = K_obj − K_ill (式1)
由于 K_rec 的极限为衍射极限所对应的截止频率 K _max。而对远场照明光的空间频率同样受到衍射极限的限制, 即 K_ill 的极值也是 K_max. 因此, 该方案中能够获取的样品空间频率的理论极限为2K_max, 即分辨率提升 1 倍。若需进一步提升成像分辨率, 则只能选择空间频率更高的倏逝波作为照明光场。
分辨率(Resolution)用瑞利判据
- Δd = 0.61λ/NA
物镜的截止频率(K_max)
- K_max = 2NA/λ
物镜能通过的最高空间频率,超过此频率的光学信息无法被捕获。
阿贝成像理论(Abbe’s Theory)
- 物体可分解为不同空间频率的正弦光栅分量。
- 物镜的孔径相当于低通滤波器,仅允许低频分量通过(K ≤ K_max)。
样品空间频率 K_obj 的计算


倏逝波提高成像分辨率
- 若倏逝波的空间频率为K_evan ,则成像系统能接收的最高频率为K_evan + K_obj,因此最小可分辨距离Λ_min 为:
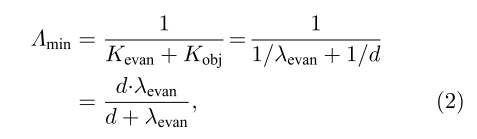
其中, λ_evan 为照明倏逝波的波长, d为物镜能分辨的最小距离. 因此在物镜已经确定的情况下, 可通过缩短照明倏逝波的波长来不断提升系统的成像分辨率。
空间移频成像中的频谱移动示意图
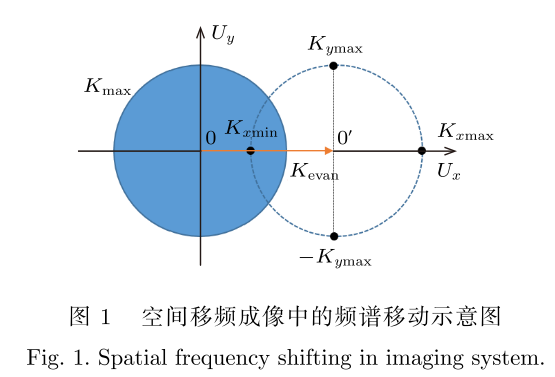
- 在图 1 所示的成像频谱空间中, 物镜原本能够接收的空间频率范围为蓝色圆形部分, 其最大值为 K_max. 若照明倏逝波的波矢为沿 x轴的 K_evan,经过移频后,则物镜能够成像的频谱范围整体向右平移,如图 1 中虚线包括的范围。
- 因此, 在基于近场照明的移频成像系统中, 沿倏逝波波矢方向可获得超越衍射极限的分辨率, 而在与之垂直的方向上, 其分辨率不会发生改变, 即系统在各个方向上分辨率不同。
SFSSRI 技术中存在两个关键问题
SFSSRI 技术中存在两个关键问题:如何缩短倏逝波的波长,以进一步提升系统的成像分辨率;如何解决成像系统的分辨率方向差异性。
倏逝波的产生及其波长、波矢
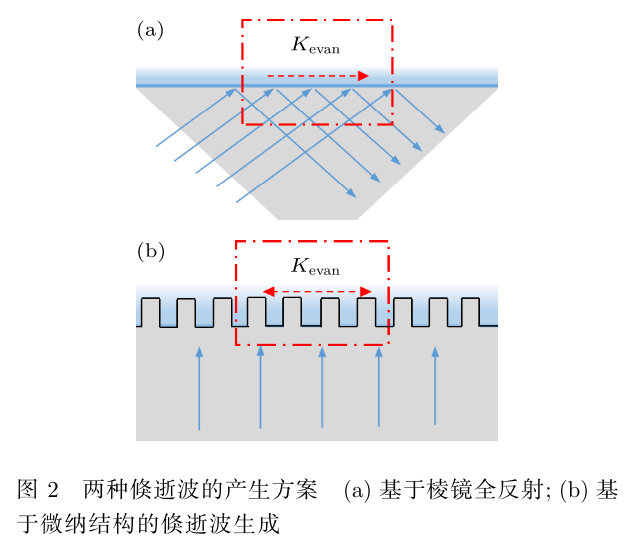
- 倏逝波的产生在 SFSSRI 技术中至关重要, 而最常见的方式为利用直角棱镜的全反射来生成倏逝波, 如图 2(a) 所示. 光线垂直入射进入棱镜, 在棱镜的上表面发生全反射, 即在棱镜的上方出现了一层向右传播的倏逝场, 记作K_evan, 其在垂直方向上振幅呈指数衰减, 因此可渗透的深度约为一个波长的距离. 生成的倏逝波波长与棱镜的折射率以及入射角有关, 可表示为:
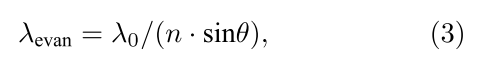
其中 λ0 为入射光的波长,n为棱镜的折射率, 而θ 为发生全反射时的入射角。由此可见,全反射时倏逝波的波长受到棱镜折射率和入 射角度的限制,无法不断缩短,因此近场照明成像系统的分辨率也无法不断提升。
- 而另一种产生倏逝波的方法为微纳结构对光场的调制,如图 2(b) 所示。当平面波从基底入射到带有微纳结构的上表面时,由于微纳结构的折射率调制,使得透射光的波前被调制,从而形成了带有高频空间信息的倏逝波。经过一段距离的传输,倏逝场的振幅按指数衰减,只剩下传播场信息,即在距离微纳结构一个波长以内的近场区域,同时包含倏逝场和传播场,而在远场区域仅有传播场。
两种倏逝波产生方案的差异
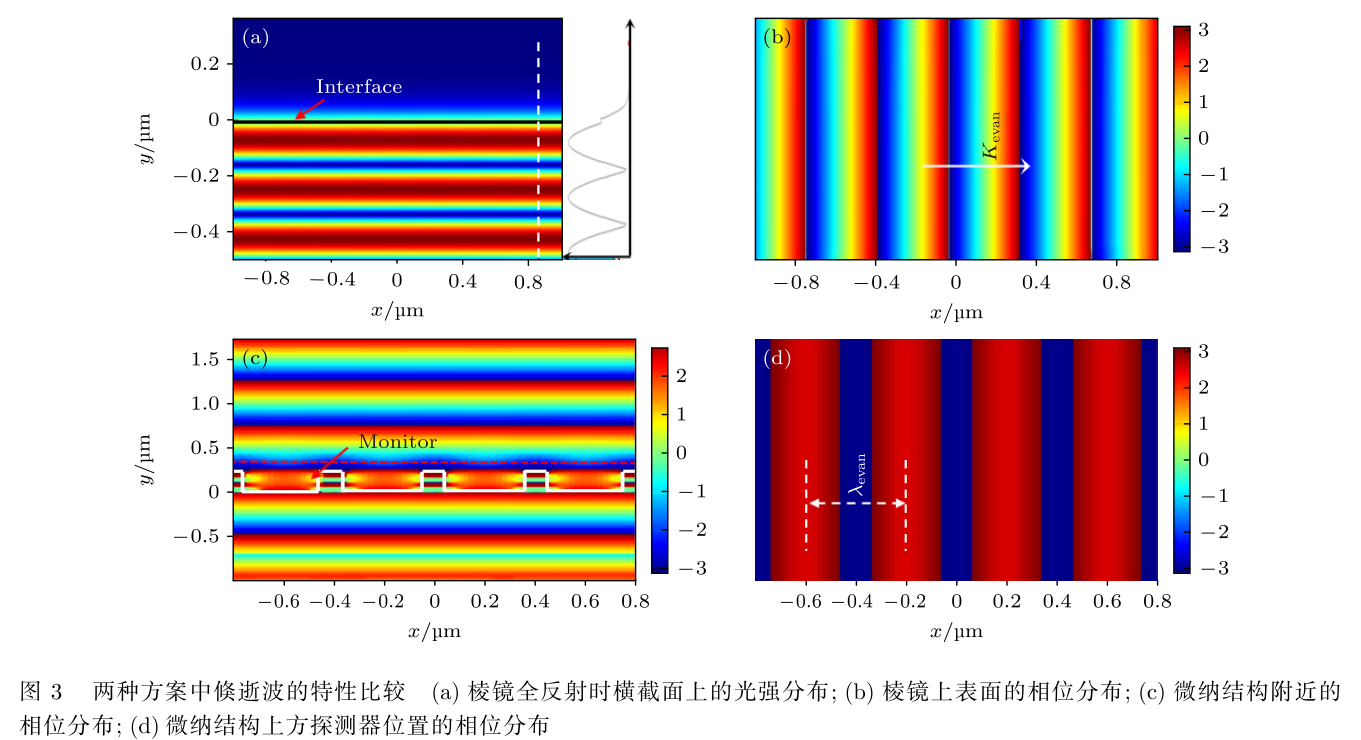
- 为对比两种方案所产生倏逝波的特性差异,将二者在分界面处的光强分布和相位分布进行仿真,如图 3 所示。当波长为 500 nm的平面波以 45°入射在 n = 2.0 的棱镜上表面全反射时,分界面下方的光强为入射光和反射光干涉形成的条纹,而分界面上方的光强呈指数衰减,如图 3(a) 所示。图 3(b)为分界面上的光场相位分布,根据等相位面可知倏逝波的波矢方向向右,其波长约为 350 nm,与(3) 式的计算结果一致。
- 与棱镜全反射模型相比,利用微纳结构产生的倏逝波无法与透射场分开, 即在微纳结构上方的近场区域内既存在倏逝波也有传播波。例如采用周期为 400 nm、线宽 100 nm,深度 400 nm, 折射率为 3 的矩形光栅作为倏逝波生成器,若波长为 500 nm的平面波垂直入射后,其表面的相位分布如图 3(c) 所示。在近场区域,原本的平面波前受到微纳结构的调制,变成了携带高频空间信息的正弦型波前; 而当远离微纳结构时,高频信息丢失,其波前又恢复为平面。将探测器放置在微纳结构上方的近场区域,可获得其相位分布,如图 3(d) 所示。两个相邻的等相位面之间的间隔为倏逝波的波长, 恰好等于微纳结构的周期,波矢方向为垂直于等相位面的方向。因此,可通过更加精细的微纳结构来获取更短波长的倏逝波。
SFSSRI 仿真模型示意图
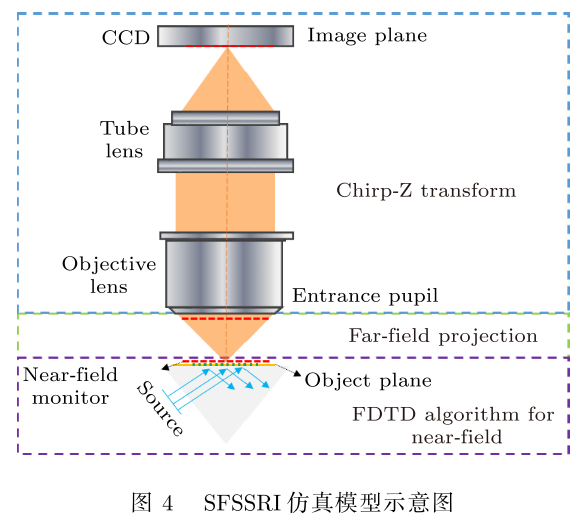
- 根据 SFSSRI 的过程,可将其分为 3 个部分:倏逝波的产生及其与样品的相互作用;样品表面的光场传输至焦平面;焦平面上的光场分布经过透镜组后到达像面,在 CCD上成像,如图 4 所示。无论是棱镜全反射、还是微纳结构模型,均可以使用时域有限差分法(finite-difference time-domain algorithm, FDTD) 来仿真倏逝波的产生,以及倏逝波与微纳结构的相互作用;
SFSSRI 特性的验证
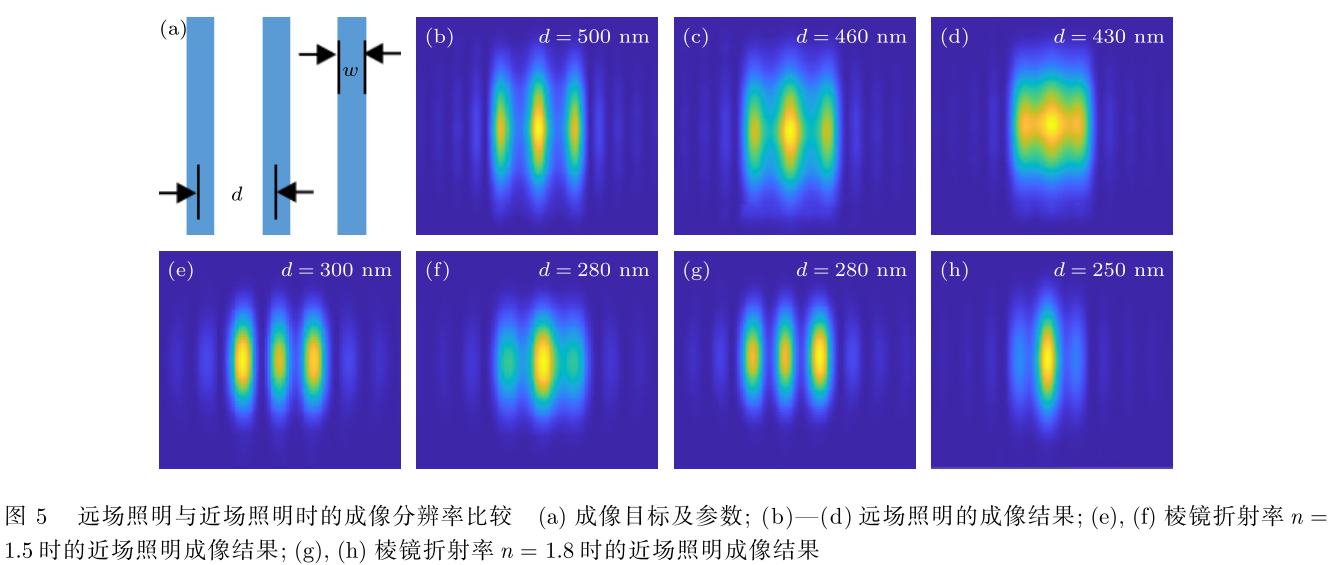
- 为验证成像模型的正确性,选择了一组 3 条线的成像样品,线条宽度为 100 nm,相邻线条的中心间隔为 d,如图 5(a) 所示。仿真中使用的入射光波长为500 nm,物镜的数值孔径(numerical aperture,NA) 为 0.9。首先,用平面波直接照明成像样品,验证远场照明时系统的成像分辨率。当线条间隔为500 nm时,3 条线可以清晰成像,如图 5(b) 所示;当线条间隔缩小至 460 nm时,3 线条恰好可分辨,如图 5(c) 所示;继续缩小线条间距至 430 nm时,3 条线的中心位置连为一体,线条无法分辨,如图 5(d)所示。
- 由此可见系统的最小可分辨距离约为 460 nm,与理论值基本一致。随后, 使用全反射时棱镜上表面的倏逝波来照明样品,棱镜的折射率 n = 1.5,其成像结果如图 5(e) 和图 5(f) 所示。当线条间隔为 300 nm时,3 条线可以清晰分辨,而当间隔缩短至 280 nm时,3 条线隐约可见。相比远场照明,倏逝波的近场照明显著提升了系统的成像分辨率。若提升棱镜的折射率至 n = 1.8,则系统的成像分辨率可进一步提升,间隔为 280 nm的样品仍然可清晰分辨,而间隔为 250 nm时无法分辨,如图 5(g)和图 5(h) 所示。根据 (3) 式,全反射时倏逝波的波长由棱镜的折射率和入射角决定,无法继续缩短,因此, 要进一步提升成像分辨率, 就必须另辟蹊径,以产生更短波长的倏逝波。
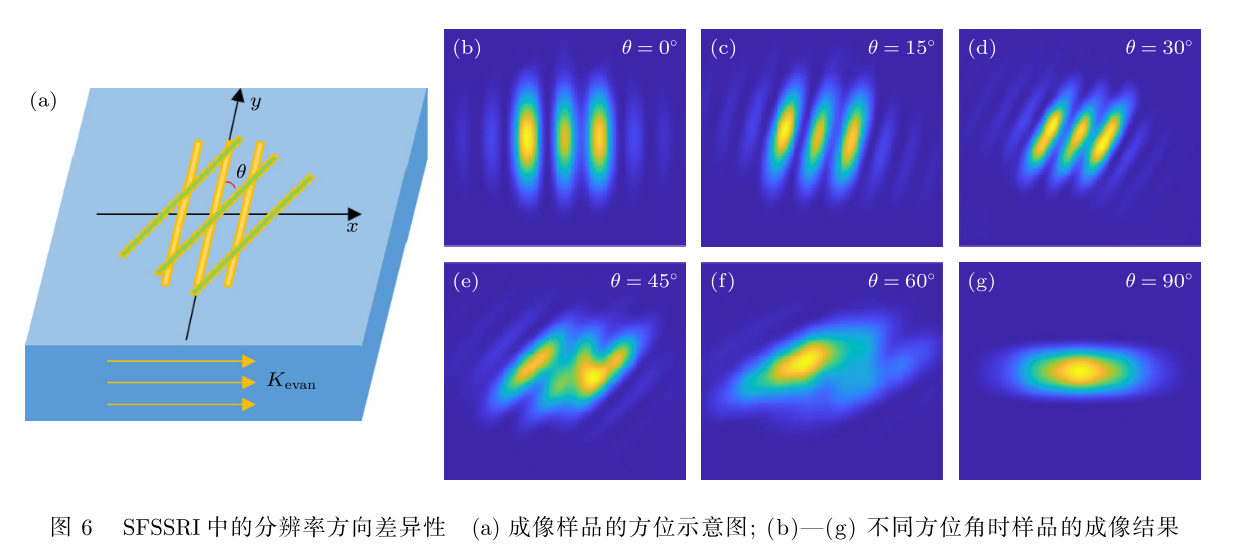
- 为验证空间移频成像中分辨率的方向差异性,继续选用线宽 100 nm、间隔 300 nm的线状样品进行测试。样品方向与棱镜表面所产生的倏逝波波矢如图 6(a) 所示, 其中倏逝波沿 x轴方向传播,线条方向与 y轴的夹角为 θ。当 θ = 0°时, 线条方向与倏逝波的波矢方向垂直,此时成像结果中 3 条线清晰可辨,如图 6(b) 所示;
- 整体旋转样品,保持线条的间距不变,成像结果如图 6(c)—(g) 所示。 随着样品方向的改变,其成像结果中 3 条线逐渐变得模糊, 当 θ > 30°时,3 条线无法分辨。由此可见,在倏逝波的波矢方向上,成像分辨率较高,其极限分辨率取决于倏逝波的波长, 而在与之垂直的方向上,分辨率最低,与远场照明时的分辨率无异。
新型倏逝波生成器及其在 SFSSRI 中的应用
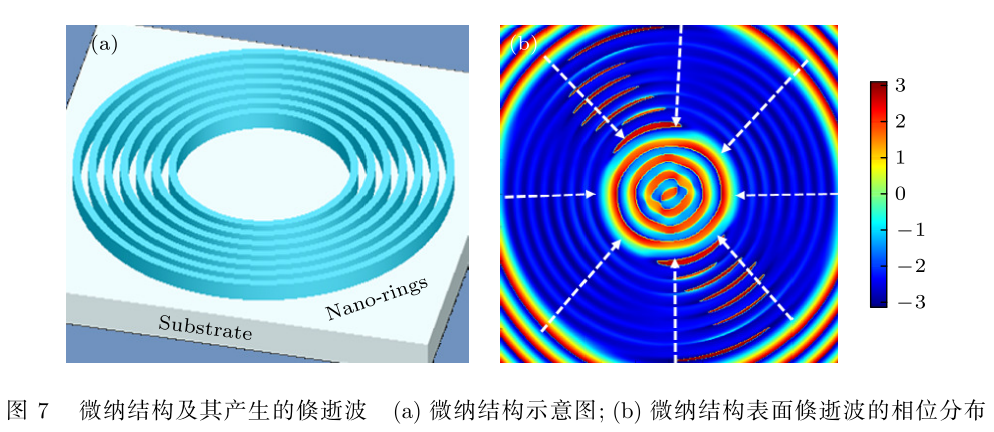
- 为解决基于棱镜全反射的倏逝波生成器中出现的上述问题,提出一种新型倏逝波生成器,如图 7(a) 所示。其核心部件为透明基底上的同心圆环形状的微纳结构 (周期 300 nm, 线宽 150 nm,深度 200 nm, 折射率为 2),圆环中心半径 1 μm的圆形区域不设微纳结构;相邻圆环间的间隔可调控倏逝波的波长;圆环的折射率和厚度可调制近场区域相位差的大小。由于该结构的旋转对称性,可生成具有全方向波矢的倏逝波,即圆环中心位置的光场具有任意方向的波矢,因此可解决棱镜全反射模型中的分辨率方向差异性问题。其生成倏逝波的相位分布如图 7(b) 所示,其中蓝色部分为微纳结构对平面波前调制后的结果;中心区域的相位为倏逝波向内传输形成的相位分布;白色箭头方向垂直于等相位面,为波矢方向。
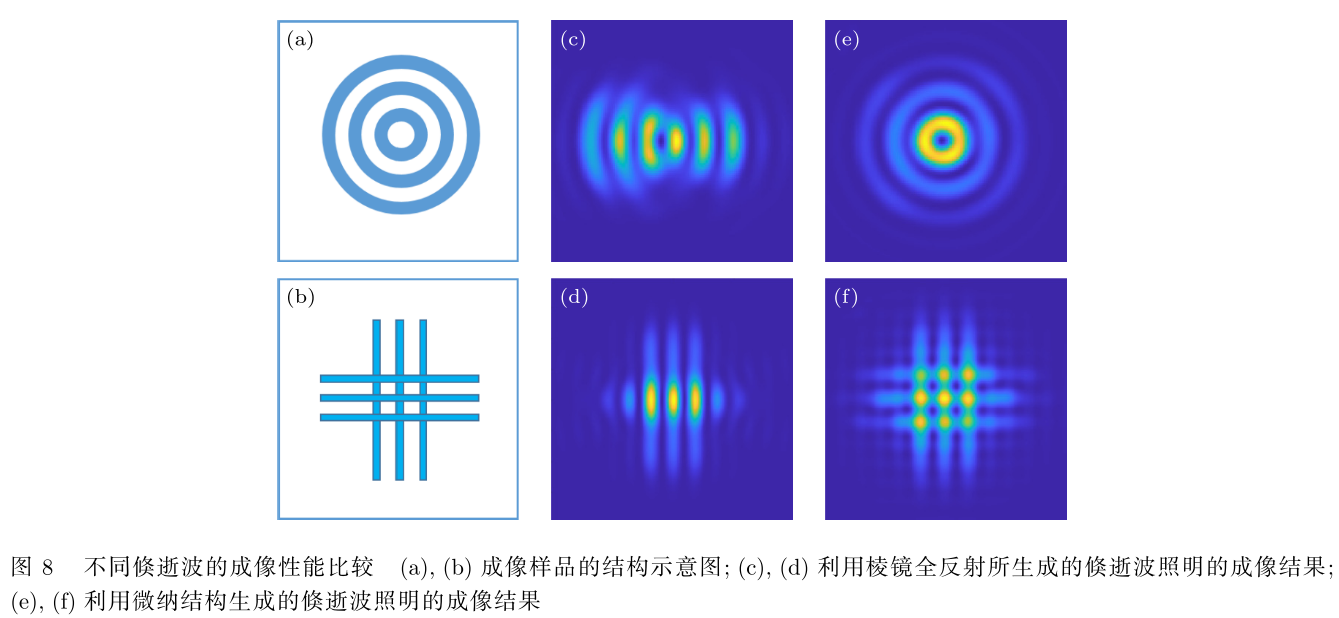
- 将上述微纳结构中心区域生成的倏逝波用于近场照明成像,并与棱镜全反射时生成的倏逝波照明成像进行比较,可看出二者的明显区别。分别选择线宽 150 nm、周期 300 nm的一组同心圆环和线宽 100 nm、周期 300 nm的一组十字条纹作为成像目标,如图 8(a) 和图 8(b) 所示。
- 利用棱镜全反射时产生的倏逝波进行照明,其成像结果如图 8(c) 和图 8(d) 所示,从图中可看出不同方向的分辨率差异以及图像的强度差异;改用上述微纳结构中心区域的倏逝场近场照明,其成像结果如图 8(e) 和图 8(f) 所示,其成像分辨率和成像强度在各方向基本一致,因此可避免因倏逝波方向单一而带来的分辨率方向差异性。
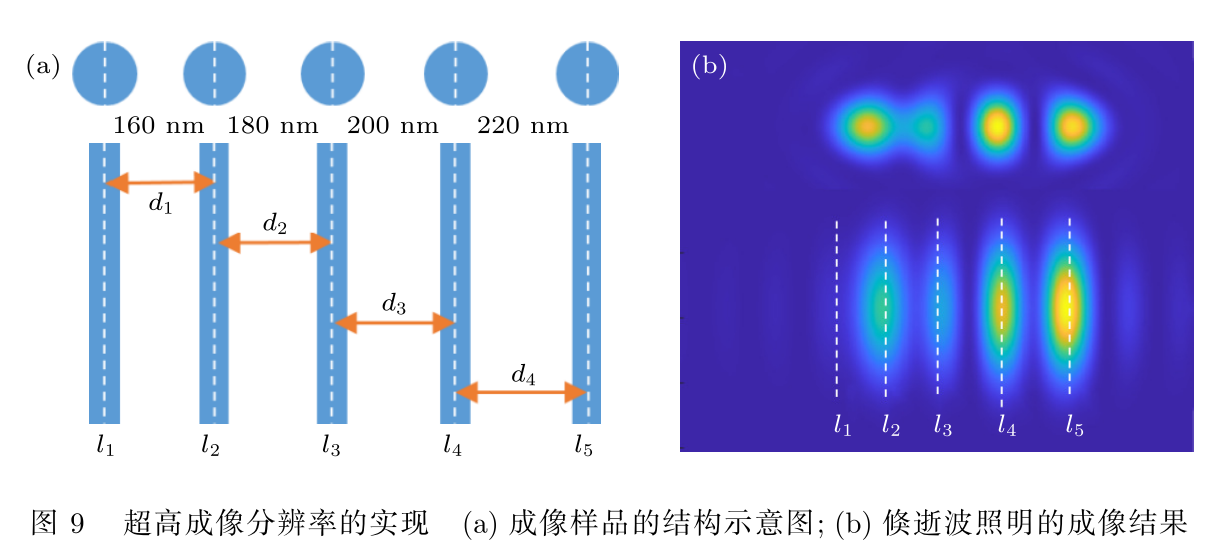
- 最后,为验证基于微纳结构产生的超短倏逝波具有极高的成像分辨率,选择线宽 100 nm, 周期200 nm,深度 200 nm,折射率为 2 的一维矩形光栅结构作为倏逝波生成器,将其生成的波长为200 nm的倏逝波用于近场照明成像。远场入射光波长为 500 nm,显微物镜的数值孔径为 0.9。成像样品为间距渐变的线状样品和点状样品,其结构参数如图 9(a) 所示,最小间隔为 160 nm,最大间隔为 220 nm。成像结果如图 9(b) 所示,从图中可以看出,当相邻线条的中心间距大于 180 nm条线可分辨。若中心间距小于 180 nm时, 则两条线相互融合,无法分辨。换点状目标后,有类似的成像效果。因此,最小可分辨距离为 180 nm, 与(2) 式中的理论预测基本一致。
附录与补遗
论文中可以引用的部分
关于文献
题目及期刊
题目:基于倏逝波照明的空间移频超分辨成像技术研究
期刊:物理学报
引用
-
作者信息
作者:凌进中, 郭金坤,王昱程,刘鑫,王晓蕊
发表时间
日期:2023年
阅读时间
日期:2025年3月19日
开源代码及其它
GitHub:无。
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 YuJiang's Long Holiday!
