论文主体思路

论文主要贡献

  1. 提出了一种由六边形孔组成的二维光栅，它可以完全抑制第二，第三和第四阶衍射。我们的光栅的六边形孔比正弦孔更容易制作[18，19]。
  2. 首先，我们从理论上分析了二维光栅的衍射特性与结构参数的关系，六角孔的特殊尺寸导致了我们所期望的衍射图样。
  3. 然后，我们从理论和实验上证明了二维光栅的衍射图样具有有效的抑制高阶衍射。

二维六角形孔光栅的理论分析和结构设计

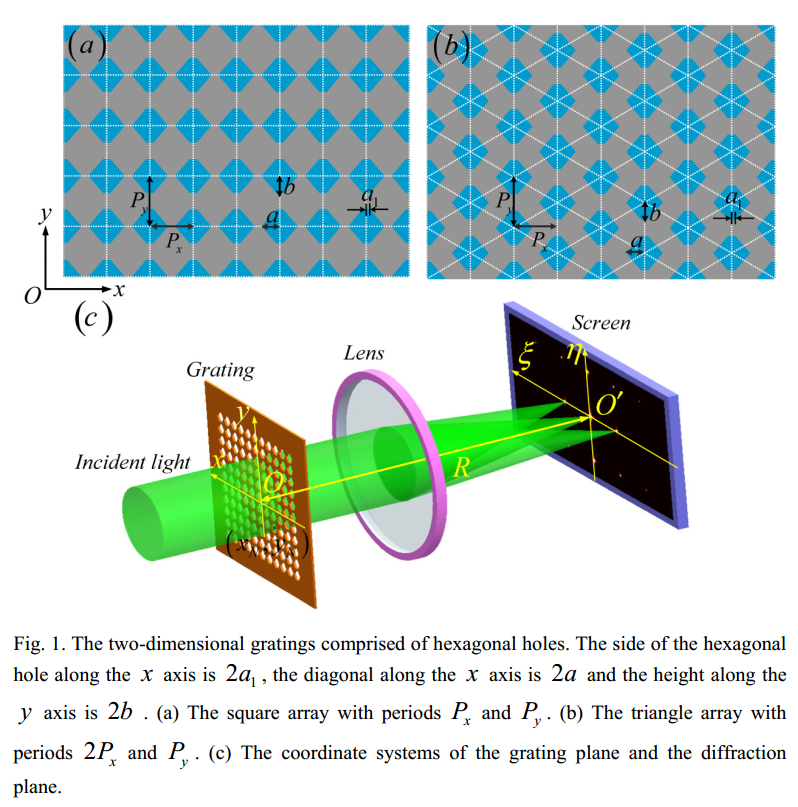
  1. 二维光栅由六边形孔组成。六边形孔沿x轴的边沿着为2a1，沿x轴的对角线沿着为2a，沿y轴的高度沿着为2b。（a）周期为Px和Py的正方形阵列。（B）周期为2Px和Py的三角形阵列。（c）光栅平面和衍射平面的坐标系。

对于包含大量相同且类似取向的孔的膜，夫琅和费衍射图案中的光分布由下式给出：

六边形孔的正方形阵列的衍射强度

如图1（a）所示的六边形孔的正方形阵列，衍射强度图案：

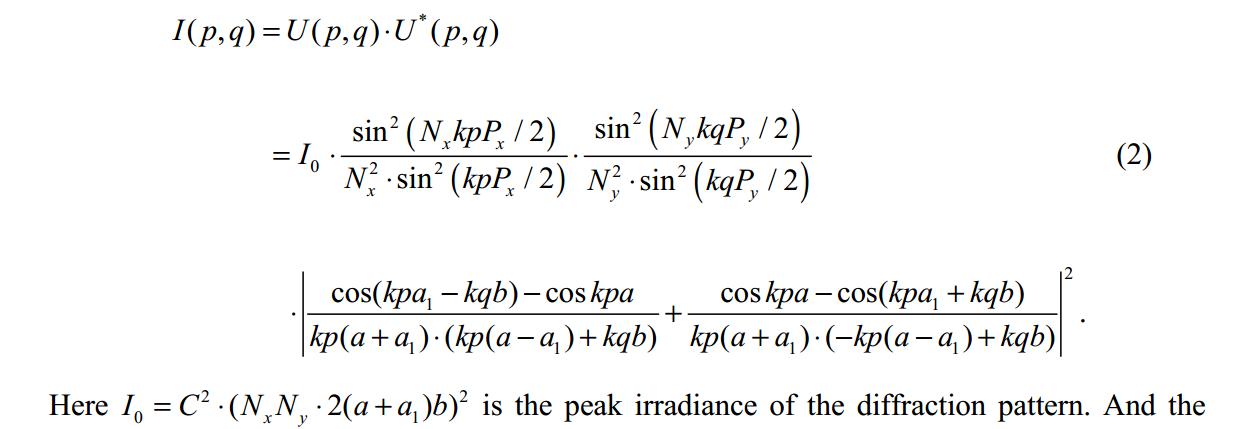
Io是衍射图案的峰值辐照度。

m级衍射强度与六边形形状的关系

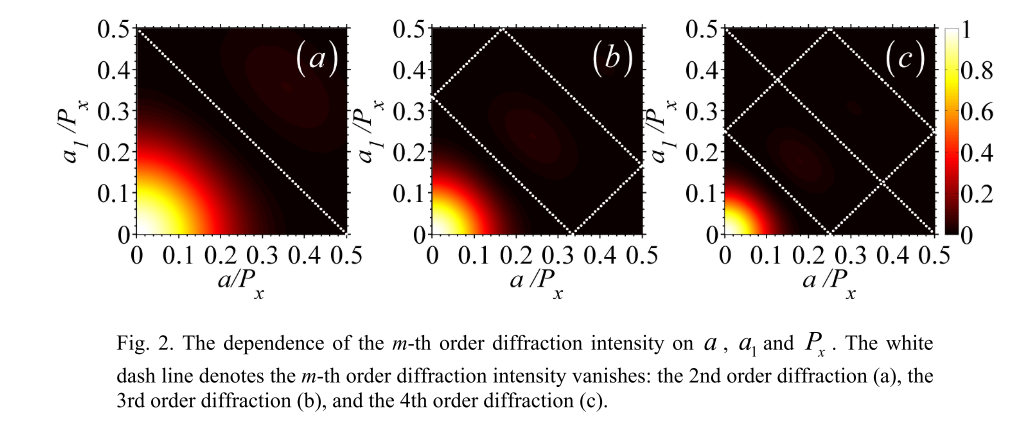
正方形六角形孔阵列的远场衍射强度图

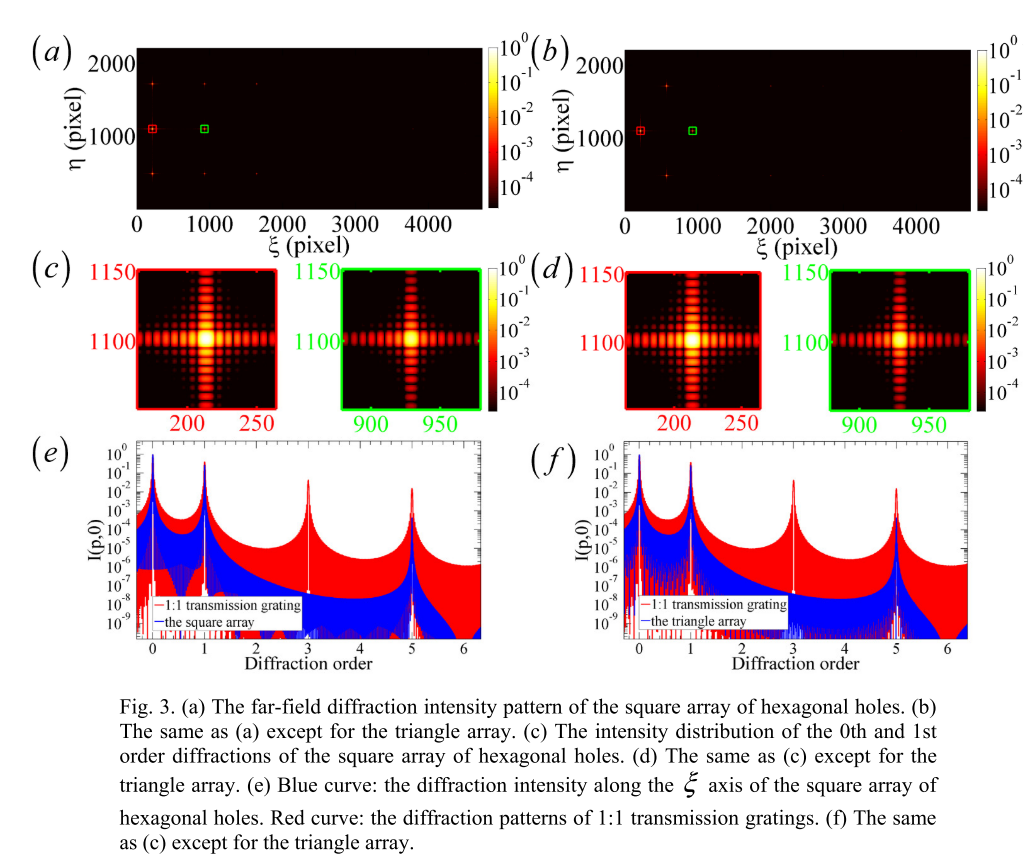
正方形六角形孔阵列的远场衍射强度图

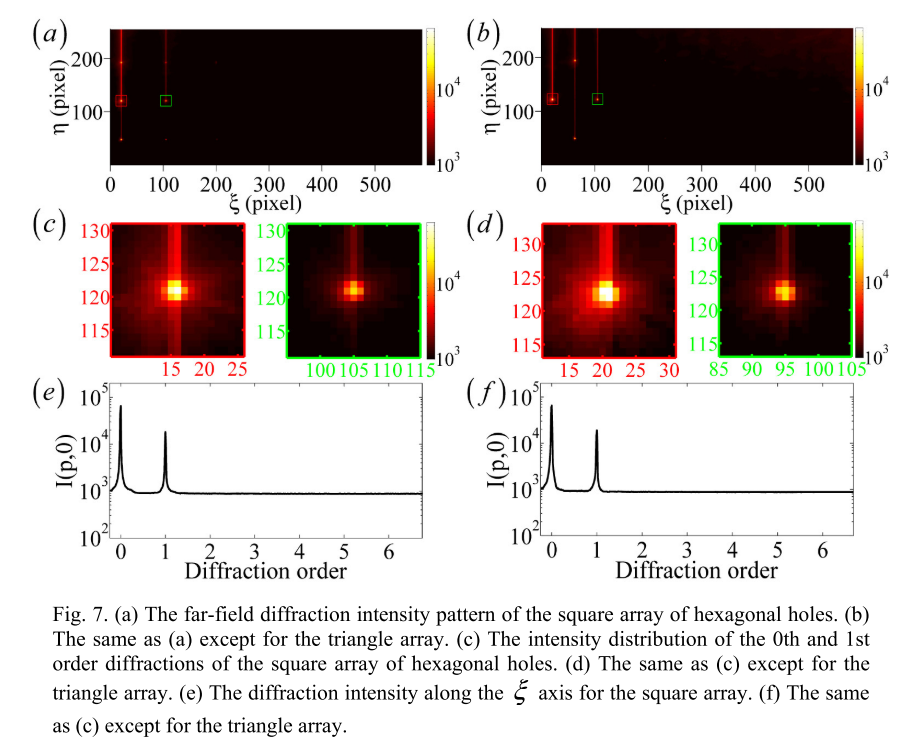
  1. (b)与(a)相同，除了三角形数组。(c)正方形六角形孔阵列的0级和1级衍射的强度分布。(d)与（c）相同，除了三角形数组。(e)正方形阵列沿光轴沿着的衍射强度。(f)与（c）相同，除了三角形数组。

附录与补遗

用傅里叶光学来解释光栅衍射

衍射场的复振幅是孔径函数的傅里叶变换。光强则是复振幅的模平方。

  1. 光栅的衍射现象可以用傅里叶光学来解释。当光通过光栅时，光栅的结构相当于一个周期性变化的透射函数，这会使得入射光波前被调制，产生不同级次的衍射光束。根据傅里叶变换的性质，周期性结构会生成离散的衍射级次，每个级次对应不同的空间频率成分。
  2. 在光学中，空间频率通常指的是物体结构在空间上的变化频率，高空间频率对应细节或边缘信息，低空间频率则对应整体或缓慢变化的结构。光栅本身的周期结构决定了其空间频率，衍射级次越高，对应的空间频率也越高，因为它们反映了更精细的结构变化。

倏逝波

  1. 传统光学显微镜的分辨率受到阿贝极限的限制，大约为波长的一半，这是因为传统显微镜只能收集传播波（propagating waves），而丢失了携带高空间频率信息的倏逝波（evanescent waves）。倏逝波的强度随着距离迅速衰减，所以通常只能在物体表面附近探测到，比如在近场扫描光学显微镜（NSOM）中。但NSOM需要物理上接近样品，扫描速度慢，应用受限。

高阶衍射的不同利用场景

高阶衍射确实携带更高空间频率的信息，但实际是否“有用”取决于应用场景：

  • 需要抑制时：避免噪声、提高能量利用率（如激光、光谱分析）。
  • 需要利用时：提取超分辨细节或增强传感灵敏度。

论文中可以引用的部分

  1. 近年来，光子筛因其新颖的特性，如超分辨聚焦和渐逝区以外的成像而引起了人们的极大关注[21-26]。光子筛的核心思想是通过设计孔的位置来产生相长或相消干涉。在这一点上，光子筛类似于具有槽位调制的单级衍射光栅。

关于文献

题目及期刊

题目：Two-dimensional gratings of hexagonal holes for high order diffraction suppression

抑制高阶衍射的二维六角形孔光栅

期刊：Optics Express

引用

  • Liu, Ziwei, et al. “Two-Dimensional Gratings of Hexagonal Holes for High Order Diffraction Suppression.” Optics Express 25.2 (2017). Print.

作者信息

作者：Z. Liu, L. Shi, T. Pu, H. Li, J. Niu, G. Wang, et al.

发表时间

日期：2017年

阅读时间

日期：2025年3月5日

开源代码及其它

GitHub：无